Last updated : October 4, 2024

Chemical Kinetics : Rate of Reaction, Rate Law Expression, Rate Constant, Order of Reaction, Molecularity, Half-Life, Arhenius Eqn, Collision Theory

Rate of Reaction

Change in concentration (reactant or product) per unit time.

Rate = \frac{Change in concentration}{Time taken}

Rate of appearance or disappearance of substance

2 A + B \to 3 C

Rate of A $(r_{A}) = - \frac{dA}{dt}$

Rate of B $(r_{B}) = - \frac{dB}{dt}$

Rate of C $(r_{C}) = + \frac{dC}{dt}$

But, Rate of A ≠ Rate of B ≠ Rate of C ≠ Rate of Reaction

- \frac{r_{A}}{2} = - r_{B} = \frac{r_{C}}{3}

Rate of rxn. (\frac{dR}{dt}) = - \frac{r_{A}}{2} = - r_{B} = \frac{r_{C}}{3}

Factors Affecting Rate of Reaction

Rate depends upon experimental conditions such as concentration of reactants (partial pressure in case of gases), temperature and catalyst.

Rate Law Expression

Concentration Dependence of Rate of Reaction

Representation of rate of reaction in terms of molar concentration of the reactants.

aA + bB \to cC + dD

Rate \propto {[A]}^{x} {[B]}^{y}

Rate = K {[A]}^{x} {[B]}^{y}

Where x and y may or may not be equal to stoichiometric coefficients (a and b).

Example :

2 A + B \to 2 AB

Experiment	Initial [A] mol L^-1	Initial [B] mol L^-1	Initial rate of formation of AB mol L^-1 s^-1
1.	0.30	0.30	0.096
2.	0.60	0.30	0.384
3.	0.30	0.60	0.192
4.	0.60	0.60	0.768

Rate law expression for this reaction
$Rate = K {[A]}^{2} [B]$

In the above reaction exponent of the concentration terms are same as their stoichiometric coefficients.

Some other examples :

\begin{array}{lcl} Reaction & Experimental rate expression \\ {CHCl}_{3} + {Cl}_{2} \to {CCl}_{4} + HCl & Rate = K [{CHCl}_{3}] {[{Cl}_{2}]}^{\frac{1}{2}} \\ {CH}_{3} {COOC}_{2} H_{5} + H_{2} O \to {CH}_{3} COOH + C_{2} H_{5} OH & Rate = K {[{CH}_{3} {COOC}_{2} H_{5}]}^{1} {[H_{2} O]}^{0} \end{array}

In these reactions, the exponent of concentration terms are not same as their stoichiometric coefficients. Thus,

Ratr law cannot be predicted just by looking at the balanced chemical equation, but must be determined experimentally.

Order of Reaction

Order : Sum of the powers of the concentration terms of the reactants in the rate law expression.

aA + bB \to cC + dD

Rate = K {[A]}^{x} {[B]}^{y}

Order (n) = x + y

x and y indicates the snesitivity of the Rate with change in concentration of A and B.

Units of Rate Constant :

\begin{array}{rcl} K & = & \frac{Rate}{{[A]}^{x} {[B]}^{y}} \\ = & \frac{concentration}{time} \times \frac{1}{{(concentration)}^{n}} (where, n = order = x + y) \end{array}

Reaction	Order	Units of rate constant
Zero order	0	$\frac{mol L^{- 1}}{s} \times \frac{1}{{(mol L^{- 1})}^{0}} = mol L^{- 1} s^{- 1}$
First Order	1	$\frac{mol L^{- 1}}{s} \times \frac{1}{{(mol L^{- 1})}^{1}} = s^{- 1}$
Second order	2	$\frac{mol L^{- 1}}{s} \times \frac{1}{{(mol L^{- 1})}^{2}} = {mol}^{- 1} L s^{- 1}$

Molecularity of Reaction

Total Number of reactant species which collide simultaneously in a elementory reaction.

Unimolecular : ${NH}_{4} {NO}_{2} \to N_{2} + 2 H_{2} O$
Bimolecular : $2 HI \to H_{2} + I_{2}$
Trimolecular : $2 NO + O_{2} \to 2 {NO}_{2}$

Maximum molecularity = 3, because probability of more than 3 molecules to collide simultaneously in a elementory reaction is very small.

Molecularity cannot be zero, negative, or fractional.

Therefore, a balanced reaction involving more than 3 molecules must take place in more than one step. When a sequance of elementory reactions forms the products, the reaction are called complex reactions.

Overall rate of a complex reaction is controlled by the slowest step, called rate determining step.

Example : Decomposition of hydrogen peroxide, catalysed by iodide ion in alkaline medium.

2 H_{2} O_{2} \to 2 H_{2} O + O_{2}

Rate = - \frac{d [H_{2} O_{2}]}{dt} = K [H_{2} O_{2}] [I^{-}]

This is a first order reaction with respect to both H₂O₂ and I^-. It take place in two steps:

$H_{2} O_{2} + I^{-} \to H_{2} O + {IO}^{-}$
$H_{2} O_{2} + {IO}^{-} \to H_{2} O + I^{-} + O_{2}$

The first step, being slow, is the rate determining step. Thus rate of formation of intermediate (IO^-) determine the rate of this reaction.

Order of a reaction is an experimental quantity. It can be zero and even a fraction but molecularity cannot be zero or a non integer.
Order is applicable to elementary as well as complex reactions whereas molecularity is applicable only for elementary reactions.
For complex reaction, order is given by the slowest step and molecularity of the slowest step is same as the order of the overall reaction.

Zero Order Reaction

Integrated Rate Equation

The rate of the reaction is proportional to zero power of the concentration of reactants.

R \to P

\begin{array}{rclcl} Rate & = & - \frac{d [R]}{dt} & = & K {[R]}^{0} \\ \Rightarrow & - \frac{d [R]}{dt} & = & K \\ \Rightarrow & d [R] & = & - K dt \\ \Rightarrow & \int_{R_{o}}^{R} d [R] & = & \int_{0}^{t} - K dt \\ \Rightarrow & [R] - [R_{o}] & = & - K t \\ \Rightarrow & [R_{o}] - [R] & = & K t \\ \Rightarrow & K & = & \frac{[R_{o}] - [R]}{t} \end{array}

K = \frac{[R_{o}] - [R]}{t}

First Order Reaction

Integrated Rate Equation

The rate of the reaction is proportional to the first power of the concentration of the reactants.

R \to P

\begin{array}{rclcl} Rate & = & - \frac{d [R]}{dt} & = & K {[R]}^{1} \\ \Rightarrow & \frac{d [R]}{[R]} & = & - K dt \\ \Rightarrow & \int_{R_{o}}^{R} \frac{d [R]}{[R]} & = & \int_{0}^{t} - K dt \\ \Rightarrow & ln [R] - ln [R_{o}] & = & - K t \\ \Rightarrow & ln \frac{[R]}{[R_{o}]} & = & - K t \\ \Rightarrow & K & = & \frac{1}{t} ln \frac{[R_{o}]}{[R]} \end{array}

[R] = [R_{o}] e^{- Kt}

K = \frac{1}{t} ln \frac{[R_{o}]}{[R]}

K = \frac{1}{(t_{2} - t_{1})} ln \frac{{[R]}_{1}}{{[R]}_{2}}

n^th Order Reaction

Half-Life of a Reaction

The half-life of a reaction is the time in which the concentration of a reactant is reduced to one half of its initial concentration.

Half-life of a zero order reaction

K = \frac{[R_{o}] - [R]}{t}

At $t = t_{1 / 2}, [R] = \frac{1}{2} [R_{o}]$

The rate constant at t_1/2 becomes

K = \frac{[R_{o}] - [\frac{R_{o}}{2}]}{t_{1 / 2}}

t_{1 / 2} = \frac{[R_{o}]}{2 K}

Half-life of a first order reaction

K = \frac{1}{t} ln \frac{[R_{o}]}{[R]}

At $t = t_{1 / 2}, [R] = \frac{1}{2} [R_{o}]$

\begin{array}{rcl} K & = & \frac{1}{t_{1 / 2}} ln \frac{[R_{o}]}{[\frac{R_{o}}{2}]} \\ t_{1 / 2} & = & \frac{1}{K} ln 2 \\ = & \frac{1}{K} 2.303 log 2 \\ = & \frac{2.303 \times 0.301}{K} \\ = & \frac{0.693}{K} \end{array}

t_{1 / 2} = \frac{0.693}{K}

For zero order reaction t_1/2 ∝ [R_o]
For first order reaction t_1/2 independent of [R_o]

Arrhenius Equation

Temperature Dependence of Rate of Reaction

Temperature dependence of rate of reaction can be accurately explained by Arrhenius equation.

K = A e^{\frac{- E_{a}}{RT}}

For a chemical reaction with raise in temperature by 10^o, the rate constant is nearly doubled.

Potential energy vs Reaction coordinate (NCERT diagram)

\begin{array}{rcl} K & = & A e^{\frac{- E_{a}}{RT}} \\ ln K & = & ln A - \frac{E_{a}}{RT} \end{array}

Rate constant at temperature T₁,

ln K_{1} = ln A - \frac{E_{a}}{{RT}_{1}} eq ... (i)

Rate constant at temperature T₂,

ln K_{2} = ln A - \frac{E_{a}}{{RT}_{2}} eq ... (ii)

Subtracting equation (i) from (ii),

\begin{array}{rcl} ln K_{2} - ln K_{1} & = & \frac{E_{a}}{{RT}_{1}} - \frac{E_{a}}{{RT}_{2}} \\ ln \frac{K_{2}}{K_{1}} & = & \frac{E_{a}}{R} [\frac{1}{T_{1}} - \frac{1}{T_{2}}] \\ 2.303 log \frac{K_{2}}{K_{1}} & = & \frac{E_{a}}{R} [\frac{T_{2} - T_{1}}{T_{1} T_{2}}] \\ log \frac{K_{2}}{K_{1}} & = & \frac{E_{a}}{2.303 R} [\frac{T_{2} - T_{1}}{T_{1} T_{2}}] \end{array}

log \frac{K_{2}}{K_{1}} = \frac{E_{a}}{2.303 R} [\frac{T_{2} - T_{1}}{T_{1} T_{2}}]

Catalysis

Effect of Catalyst on Rate of Reaction

A catalyst is a substance which increases the rate of a reaction without itself undergoing any permanent chemical change.

The word catalyst should not be used when the added substance reduces the rate of raction. The substance is then called inhibitor.

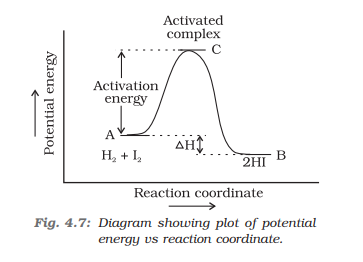
Catalyst provides an alternate pathway by reducing the activation energy between reactants and products.
From Arrhenius equation, lower the activation energy faster the rate of a reaction.
catalyst does not alter Gibbs energy, ΔG of a reaction.
It catalyses the spontaneous reactions but does not catalyse nonspontaneous reactions.
Catalyst does not change the equilibrium constant.
It helps in attaining the equilibrium faster.
It catalyses the forward as well as the backward reactions to the same extent.

Collision Theory of a Chemical Reaction

Reactant molecules are assumed to be hard spheres and reaction is postulated to occur when molecules collide with each other.

A + B \to Products

Rate = P Z_{AB} e^{\frac{- E_{a}}{RT}}

Z (collision frequency) = number of collisions per second per unit volume of the reaction mixture.
where Z_AB = collision frequancy of reactants A and B.
e^-E_a/RT = fraction of molecules with energies equal to or greater than E_a.
P (probability/steric factor) = proper orientation of reactant molecules lead to bond formation whereas improper orientation makes them simply bounce back.

# Rate of Reaction # Rate Law Expression # Order of Reaction # Molecularity # Half-Life of Reaction # Arhenius Equation # Catalysis # Collision Theory # Physical Chemistry